Mean Reflected Stochastic Differential Equations With Jumps
Résumé
This paper is devoted to the study of reflected Stochastic Differential Equations
with jumps when the constraint is not on the paths of the solution but acts on the law of the
solution. This type of reflected equations have been introduced recently by Briand, Elie and Hu
[BEH18] in the context of BSDEs, when no jumps occur. In [BCdRGL16], the authors study a
numerical scheme based on particle systems to approximate these reflected SDEs. In this paper,
we prove existence and uniqueness of solutions to this kind of reflected SDEs with jumps and
we generalize the results obtained in [BCdRGL16] to this context.
Domaines
Probabilités [math.PR]
Fichier principal
 MRSDEJ_HAL.pdf (607.58 Ko)
Télécharger le fichier
MRSDEJ_HAL.pdf (607.58 Ko)
Télécharger le fichier
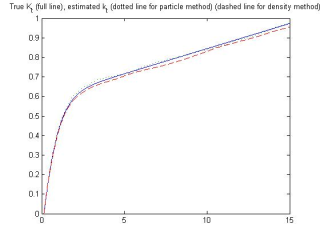 K_non_lineaire(v).jpg (19.35 Ko)
Télécharger le fichier
Ep_Black_Scholes(iv)_grandN_n=1000,N=100,100,800,L=1000.jpg (15.88 Ko)
Télécharger le fichier
Ep_grandN_Brown_Poiss(i)_Levy.jpg (15.2 Ko)
Télécharger le fichier
K_Black_Scholes(iv).jpg (19.14 Ko)
Télécharger le fichier
K_Brown_Poiss(i)_levy_edp.jpg (17.72 Ko)
Télécharger le fichier
K_non_lineaire(v).jpg (19.35 Ko)
Télécharger le fichier
Ep_Black_Scholes(iv)_grandN_n=1000,N=100,100,800,L=1000.jpg (15.88 Ko)
Télécharger le fichier
Ep_grandN_Brown_Poiss(i)_Levy.jpg (15.2 Ko)
Télécharger le fichier
K_Black_Scholes(iv).jpg (19.14 Ko)
Télécharger le fichier
K_Brown_Poiss(i)_levy_edp.jpg (17.72 Ko)
Télécharger le fichier
| Format | Figure, Image |
|---|---|
| Origine | Fichiers produits par l'(les) auteur(s) |
Loading...

